최소 신장 트리(Minimum Spanning Tree)란?
💡최소 신장 트리: 그래프에서 모든 정점에 대해 최소한의 연결만을 남긴 그래프이다. 즉 간선의 가중치 합이 가장 작은 트리를 뜻한다. 사이클이 존재하지 않아야 한다.
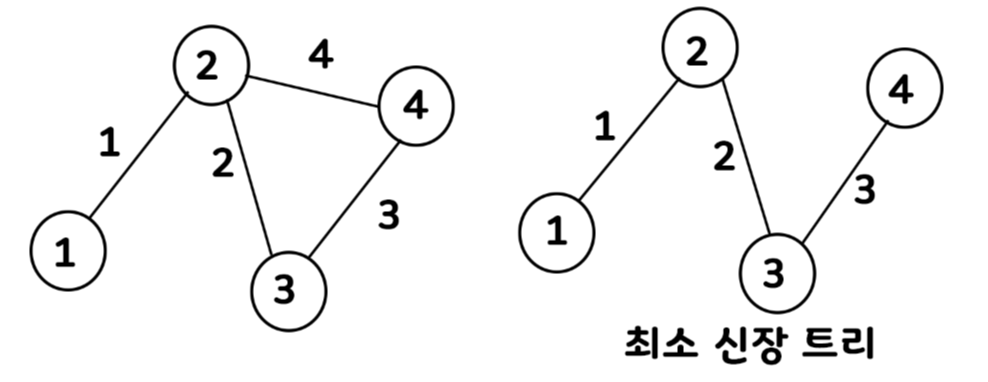
최소 신장 트리를 찾는 알고리즘으론 크루스칼 알고리즘, 프림 알고리즘이 있다. 이 알고리즘은 그리디 알고리즘 기법을 활용한 알고리즘이다.
프림 알고리즘은 바이너리 힙을 이용하는 경우 의 시간 복잡도를 가지며, 크루스칼 알고리즘은 경로 최적화를 이용하지 않는 경우 , 경로 최적화를 이용하는 경우 의 시간 복잡도를 가지기 때문에, 그래프의 간선 밀도를 고려하여 최적의 알고리즘을 선택하는 것이 필요하다.
크루스칼 알고리즘(Kruskal Algorithm)
1. 모든 간선들의 가중치를 오름차순으로 정렬한다.
2. 가중치가 가장 작은 간선을 선택한다.
3. 위에서 선택한 간선이 연결하려는 2개의 노드가 서로 연결되지 않은 상태라면, 2개의 노드를 서로 연결한다.
4. 이 과정을 반복해서 최소 신장 트리를 완성한다.
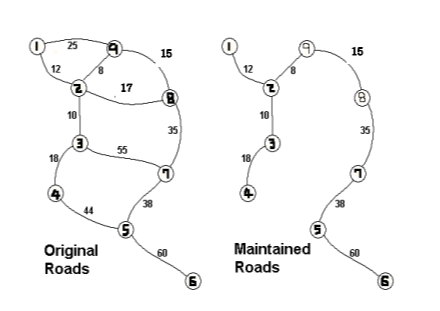
1) 가중치를 오름차 순으로 정렬 후, 작은 간선을 선택해서 트리를 이어 나간다.(Union 연산 활용) 이때, 2 정점과 8정점을 이어주는 17의 가중치를 가지고 있는 간선을 보자. 이미 2와 8은 같은 집합이다(Find 활용). 가중치를 기준으로 오름차순 정렬을 했기 때문에 2와 8 정점은 이어줄 필요가 없다.
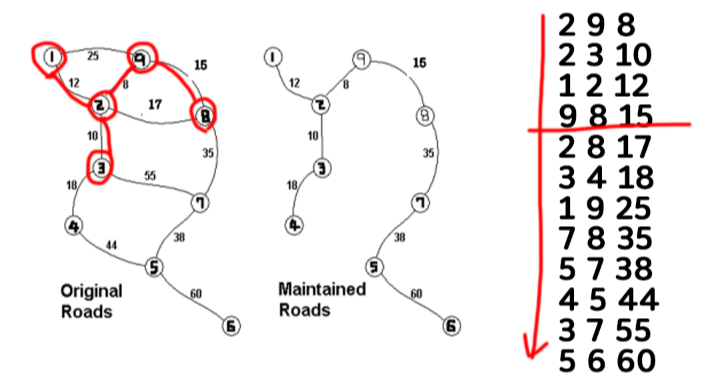
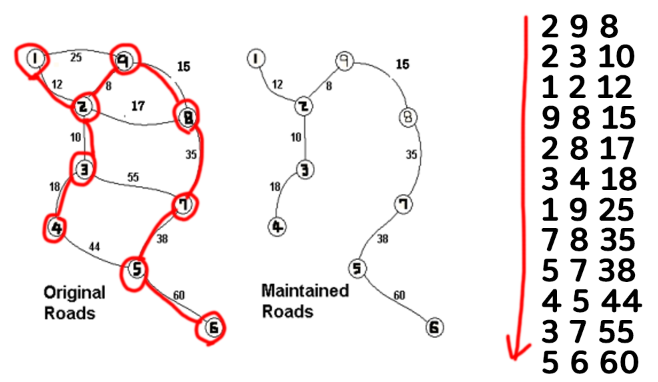
2) 이렇게 따라가다 보면, 최소 신장 트리를 구할 수 있다.
import java.util.*;
class Edge implements Comparable<Edge>{
public int v1;
public int v2;
public int cost;
Edge(int v1, int v2, int cost) {
this.v1 = v1;
this.v2 = v2;
this.cost = cost;
}
@Override
public int compareTo(Edge ob){
return this.cost-ob.cost;
}
}
class Main {
static int[] unf;
public static int Find(int v){
if(v==unf[v]) return v;
else return unf[v]=Find(unf[v]);
}
public static void Union(int a, int b){
int fa=Find(a);
int fb=Find(b);
if(fa!=fb) unf[fa]=fb;
}
public static void main(String[] args){
Scanner kb = new Scanner(System.in);
int n=kb.nextInt();
int m=kb.nextInt();
unf=new int[n+1];
ArrayList<Edge> arr=new ArrayList<>();
for(int i=1; i<=n; i++) unf[i]=i;
for(int i=0; i<m; i++){
int a=kb.nextInt();
int b=kb.nextInt();
int c=kb.nextInt();
arr.add(new Edge(a, b, c));
}
int answer=0;
Collections.sort(arr);
for(Edge ob : arr){
int fv1=Find(ob.v1);
int fv2=Find(ob.v2);
if(fv1!=fv2){
answer+=ob.cost;
Union(ob.v1, ob.v2);
}
}
System.out.println(answer);
}
}프림 알고리즘(Prim Algorithm)
다익스트라 알고리즘과 달리 음수의 가중치가 있는 경우에도 동작이 가능하다. 우선순위 큐를 이용해서 구현한다면 O((V+E)logV)의 시간 복잡도를 가진다.
-
임의의 정점을 선택하여 하나의 정점을 갖는 최초의 트리를 구성한다.
-
트리에 포함된 정점과 트리에 포함되지 않은 정점 간의 간선 중 가장 작은 가중치를 가지는 간선을 선택하여 트리에 추가한다.
-
모든 정점이 트리에 포함될 때 까지 2를 반복한다.
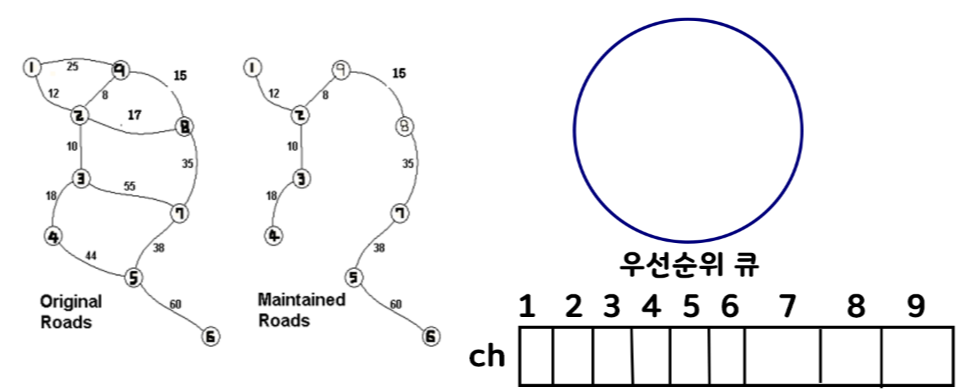
1) 보통 1번 정점에서 시작한다. 1번이 0번 정점에서 왔다고 가정하고 우선순위 큐에 값을 넣어준다. 그리고 우선 순위 큐에서 값을 뺀다음 방문했다는 표시를 남길 check배열에 방문 표시를 해준다.
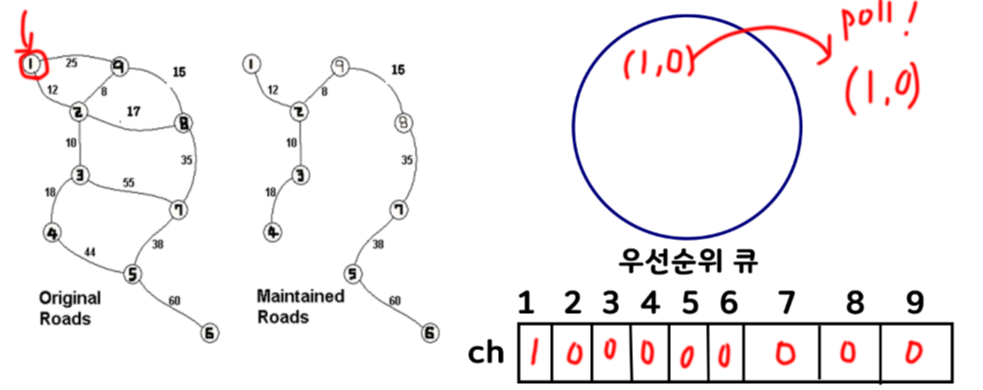
2) 다음 정점 1과 인접한 2번 정점과 9번 정점에 대한 정보를 다시 우선순위 큐에 넣어준다. 우선 순위 큐에 오름차순으로 정렬 되어 있을 테니, 제일 작은 2정점으로 가는 데이터를 poll해주고, 같은 집합인지 확인 후, 체크해준다. 누적된 가중치값은 따로 저장해준다.
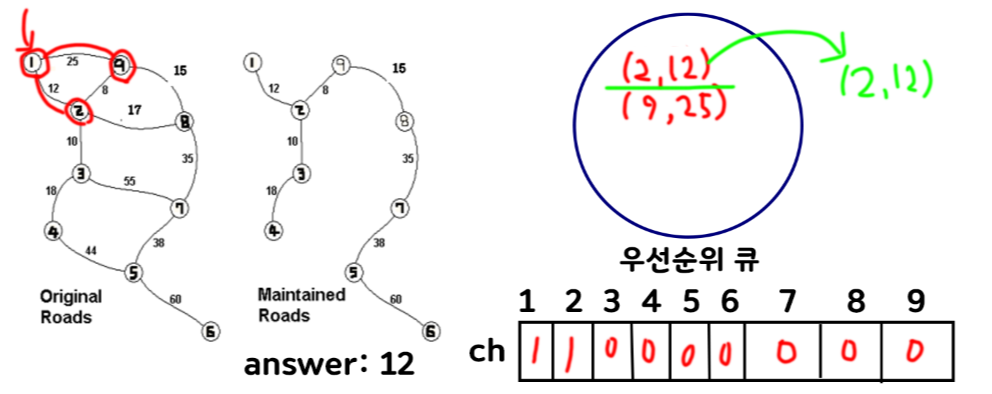
3) 위와 같은 방법으로 인접 정점과 가중치를 우선순위 큐에 넣어주며 처리하면 된다. 9번 정점으로 가는 간선의 가중치가 더 작으므로 9번 정점을 poll 해주고, 9번 정점과 인접한 (8, 15), (9, 25)를 우선순위 큐에 넣어주어 처리하면 된다.
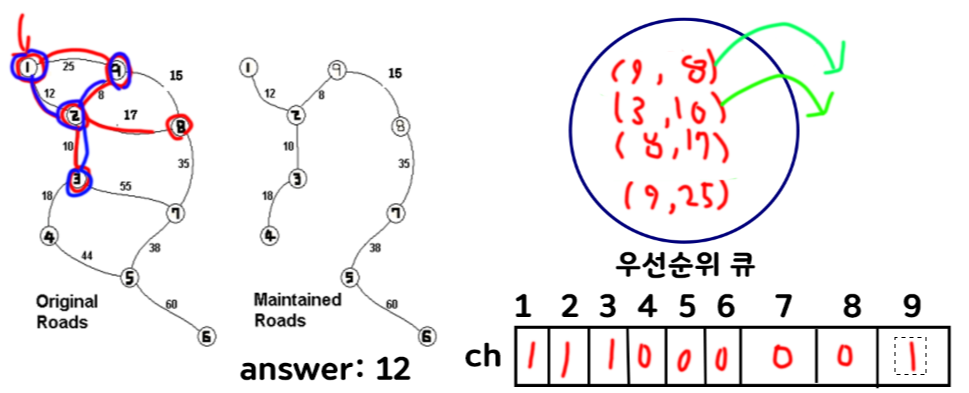
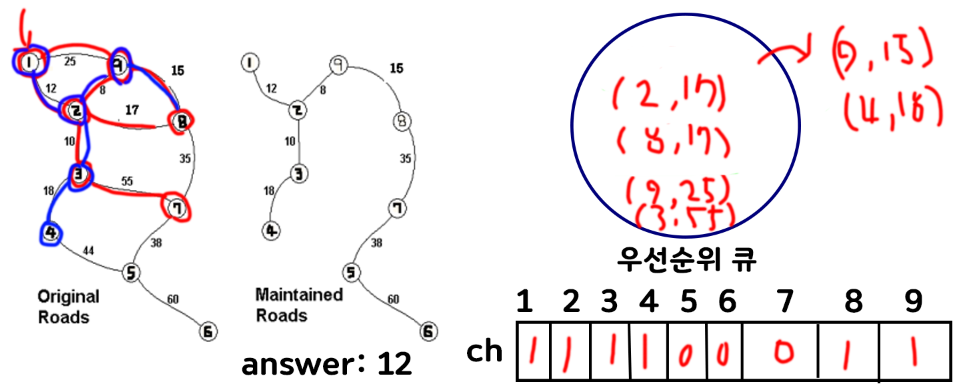
이 같은 방법으로 검사를 하다보면 최소 신장 트리를 구할 수 있다.
import java.util.*;
class Edge implements Comparable<Edge>{
public int vex;
public int cost;
Edge(int vex, int cost) {
this.vex = vex;
this.cost = cost;
}
@Override
public int compareTo(Edge ob){
return this.cost-ob.cost;
}
}
class Main {
public static void main(String[] args){
Scanner kb = new Scanner(System.in);
int n=kb.nextInt();
int m=kb.nextInt();
ArrayList<ArrayList<Edge>> graph = new ArrayList<ArrayList<Edge>>();
for(int i=0; i<=n; i++){
graph.add(new ArrayList<Edge>());
}
int[] ch=new int[n+1];
for(int i=0; i<m; i++){
int a=kb.nextInt();
int b=kb.nextInt();
int c=kb.nextInt();
graph.get(a).add(new Edge(b, c));
graph.get(b).add(new Edge(a, c));
}
int answer=0;
PriorityQueue<Edge> pQ = new PriorityQueue<>();
pQ.offer(new Edge(1, 0));
while(!pQ.isEmpty()){
Edge tmp=pQ.poll();
int ev=tmp.vex;
if(ch[ev]==0){
ch[ev]=1;
answer+=tmp.cost;
for(Edge ob : graph.get(ev)){
if(ch[ob.vex]==0) pQ.offer(new Edge(ob.vex, ob.cost));
}
}
}
System.out.println(answer);
}
}
완성 코드(프림 알고리즘, 크루스칼 알고리즘)
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
class Edge implements Comparable<Edge>{
int vex1;
int vex2;
int cost;
// 크루스칼 알고리즘에 사용할 생성자
Edge(int vex1, int vex2, int cost){
this.vex1 = vex1;
this.vex2 = vex2;
this.cost = cost;
}
// 프림 알고리즘에 사용할 생성자
Edge(int vex, int cost){
this.vex1 = vex;
this.cost = cost;
}
@Override
public int compareTo(Edge o) {
return this.cost - o.cost;
}
}
class Kruskal{
ArrayList<Edge> list;
int[] unf;
int minimumCost;
Kruskal(int v){
unf = new int[v+1];
list = new ArrayList<>();
minimumCost = 0;
for(int i = 1; i <= v; i++) unf[i] = i;
}
public int Find(int v){
if(unf[v] == v) return unf[v];
else return unf[v] = Find(unf[v]);
}
public void Union(int a, int b){
int fa = Find(a);
int fb = Find(b);
if(a != b) unf[fa] = fb;
}
public void spanningTree(){
for(Edge e : list){
int fa = Find(e.vex1);
int fb = Find(e.vex2);
if(fa != fb){
minimumCost += e.cost;
Union(e.vex1, e.vex2);
}
}
}
}
class Prim{
int minimumCost;
int[] ch;
ArrayList<ArrayList<Edge>> graph;
PriorityQueue<Edge> pQ;
Prim(int v){
minimumCost = 0;
ch = new int[v+1];
graph = new ArrayList<>();
pQ = new PriorityQueue<>();
for(int i=0; i<=v; i++){
graph.add(new ArrayList<Edge>());
}
}
public void spanningTree() {
pQ.offer(new Edge(1,0));
while(!pQ.isEmpty()){
Edge tmp = pQ.poll();
int ev = tmp.vex1;
if(ch[ev] == 0){
ch[ev] = 1;
minimumCost += tmp.cost;
for(Edge ob : graph.get(ev)){
if(ch[ob.vex1]==0) pQ.offer(new Edge(ob.vex1, ob.cost));
}
}
}
}
}
class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int v = Integer.parseInt(st.nextToken());
int n = Integer.parseInt(st.nextToken());
Kruskal kruskal = new Kruskal(v);
Prim prim = new Prim(v);
for(int i = 0; i < n; i++){
st = new StringTokenizer(br.readLine());
// a정점
int a = Integer.parseInt(st.nextToken());
// b정점
int b = Integer.parseInt(st.nextToken());
// 가중치
int c = Integer.parseInt(st.nextToken());
kruskal.list.add(new Edge(a, b, c));
prim.graph.get(a).add(new Edge(b, c));
prim.graph.get(b).add(new Edge(a, c));
}
Collections.sort(kruskal.list);
kruskal.spanningTree();
prim.spanningTree();
System.out.println(kruskal.minimumCost);
//System.out.println(prim.minimumCost);
}
}'Algorithm > 알고리즘 개념' 카테고리의 다른 글
| [알고리즘] 삽입 정렬(insertion sort) (0) | 2023.05.10 |
|---|---|
| [알고리즘] 버블 정렬(bubble sort) (0) | 2023.05.10 |
| [알고리즘] Union-Find Algorithm (유니온 파인드 알고리즘) (0) | 2023.04.04 |
| [알고리즘] Dijkstra Algorithm (다익스트라 알고리즘) (0) | 2023.04.04 |
| [알고리즘] Greedy Algorithm(탐욕 알고리즘) (0) | 2023.04.03 |
최소 신장 트리(Minimum Spanning Tree)란?
💡최소 신장 트리: 그래프에서 모든 정점에 대해 최소한의 연결만을 남긴 그래프이다. 즉 간선의 가중치 합이 가장 작은 트리를 뜻한다. 사이클이 존재하지 않아야 한다.

최소 신장 트리를 찾는 알고리즘으론 크루스칼 알고리즘, 프림 알고리즘이 있다. 이 알고리즘은 그리디 알고리즘 기법을 활용한 알고리즘이다.
프림 알고리즘은 바이너리 힙을 이용하는 경우 의 시간 복잡도를 가지며, 크루스칼 알고리즘은 경로 최적화를 이용하지 않는 경우 , 경로 최적화를 이용하는 경우 의 시간 복잡도를 가지기 때문에, 그래프의 간선 밀도를 고려하여 최적의 알고리즘을 선택하는 것이 필요하다.
크루스칼 알고리즘(Kruskal Algorithm)
1. 모든 간선들의 가중치를 오름차순으로 정렬한다.
2. 가중치가 가장 작은 간선을 선택한다.
3. 위에서 선택한 간선이 연결하려는 2개의 노드가 서로 연결되지 않은 상태라면, 2개의 노드를 서로 연결한다.
4. 이 과정을 반복해서 최소 신장 트리를 완성한다.

1) 가중치를 오름차 순으로 정렬 후, 작은 간선을 선택해서 트리를 이어 나간다.(Union 연산 활용) 이때, 2 정점과 8정점을 이어주는 17의 가중치를 가지고 있는 간선을 보자. 이미 2와 8은 같은 집합이다(Find 활용). 가중치를 기준으로 오름차순 정렬을 했기 때문에 2와 8 정점은 이어줄 필요가 없다.

2) 이렇게 따라가다 보면, 최소 신장 트리를 구할 수 있다.

import java.util.*;
class Edge implements Comparable<Edge>{
public int v1;
public int v2;
public int cost;
Edge(int v1, int v2, int cost) {
this.v1 = v1;
this.v2 = v2;
this.cost = cost;
}
@Override
public int compareTo(Edge ob){
return this.cost-ob.cost;
}
}
class Main {
static int[] unf;
public static int Find(int v){
if(v==unf[v]) return v;
else return unf[v]=Find(unf[v]);
}
public static void Union(int a, int b){
int fa=Find(a);
int fb=Find(b);
if(fa!=fb) unf[fa]=fb;
}
public static void main(String[] args){
Scanner kb = new Scanner(System.in);
int n=kb.nextInt();
int m=kb.nextInt();
unf=new int[n+1];
ArrayList<Edge> arr=new ArrayList<>();
for(int i=1; i<=n; i++) unf[i]=i;
for(int i=0; i<m; i++){
int a=kb.nextInt();
int b=kb.nextInt();
int c=kb.nextInt();
arr.add(new Edge(a, b, c));
}
int answer=0;
Collections.sort(arr);
for(Edge ob : arr){
int fv1=Find(ob.v1);
int fv2=Find(ob.v2);
if(fv1!=fv2){
answer+=ob.cost;
Union(ob.v1, ob.v2);
}
}
System.out.println(answer);
}
}프림 알고리즘(Prim Algorithm)
다익스트라 알고리즘과 달리 음수의 가중치가 있는 경우에도 동작이 가능하다. 우선순위 큐를 이용해서 구현한다면 O((V+E)logV)의 시간 복잡도를 가진다.
-
임의의 정점을 선택하여 하나의 정점을 갖는 최초의 트리를 구성한다.
-
트리에 포함된 정점과 트리에 포함되지 않은 정점 간의 간선 중 가장 작은 가중치를 가지는 간선을 선택하여 트리에 추가한다.
-
모든 정점이 트리에 포함될 때 까지 2를 반복한다.

1) 보통 1번 정점에서 시작한다. 1번이 0번 정점에서 왔다고 가정하고 우선순위 큐에 값을 넣어준다. 그리고 우선 순위 큐에서 값을 뺀다음 방문했다는 표시를 남길 check배열에 방문 표시를 해준다.

2) 다음 정점 1과 인접한 2번 정점과 9번 정점에 대한 정보를 다시 우선순위 큐에 넣어준다. 우선 순위 큐에 오름차순으로 정렬 되어 있을 테니, 제일 작은 2정점으로 가는 데이터를 poll해주고, 같은 집합인지 확인 후, 체크해준다. 누적된 가중치값은 따로 저장해준다.

3) 위와 같은 방법으로 인접 정점과 가중치를 우선순위 큐에 넣어주며 처리하면 된다. 9번 정점으로 가는 간선의 가중치가 더 작으므로 9번 정점을 poll 해주고, 9번 정점과 인접한 (8, 15), (9, 25)를 우선순위 큐에 넣어주어 처리하면 된다.


이 같은 방법으로 검사를 하다보면 최소 신장 트리를 구할 수 있다.
import java.util.*;
class Edge implements Comparable<Edge>{
public int vex;
public int cost;
Edge(int vex, int cost) {
this.vex = vex;
this.cost = cost;
}
@Override
public int compareTo(Edge ob){
return this.cost-ob.cost;
}
}
class Main {
public static void main(String[] args){
Scanner kb = new Scanner(System.in);
int n=kb.nextInt();
int m=kb.nextInt();
ArrayList<ArrayList<Edge>> graph = new ArrayList<ArrayList<Edge>>();
for(int i=0; i<=n; i++){
graph.add(new ArrayList<Edge>());
}
int[] ch=new int[n+1];
for(int i=0; i<m; i++){
int a=kb.nextInt();
int b=kb.nextInt();
int c=kb.nextInt();
graph.get(a).add(new Edge(b, c));
graph.get(b).add(new Edge(a, c));
}
int answer=0;
PriorityQueue<Edge> pQ = new PriorityQueue<>();
pQ.offer(new Edge(1, 0));
while(!pQ.isEmpty()){
Edge tmp=pQ.poll();
int ev=tmp.vex;
if(ch[ev]==0){
ch[ev]=1;
answer+=tmp.cost;
for(Edge ob : graph.get(ev)){
if(ch[ob.vex]==0) pQ.offer(new Edge(ob.vex, ob.cost));
}
}
}
System.out.println(answer);
}
}
완성 코드(프림 알고리즘, 크루스칼 알고리즘)
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
class Edge implements Comparable<Edge>{
int vex1;
int vex2;
int cost;
// 크루스칼 알고리즘에 사용할 생성자
Edge(int vex1, int vex2, int cost){
this.vex1 = vex1;
this.vex2 = vex2;
this.cost = cost;
}
// 프림 알고리즘에 사용할 생성자
Edge(int vex, int cost){
this.vex1 = vex;
this.cost = cost;
}
@Override
public int compareTo(Edge o) {
return this.cost - o.cost;
}
}
class Kruskal{
ArrayList<Edge> list;
int[] unf;
int minimumCost;
Kruskal(int v){
unf = new int[v+1];
list = new ArrayList<>();
minimumCost = 0;
for(int i = 1; i <= v; i++) unf[i] = i;
}
public int Find(int v){
if(unf[v] == v) return unf[v];
else return unf[v] = Find(unf[v]);
}
public void Union(int a, int b){
int fa = Find(a);
int fb = Find(b);
if(a != b) unf[fa] = fb;
}
public void spanningTree(){
for(Edge e : list){
int fa = Find(e.vex1);
int fb = Find(e.vex2);
if(fa != fb){
minimumCost += e.cost;
Union(e.vex1, e.vex2);
}
}
}
}
class Prim{
int minimumCost;
int[] ch;
ArrayList<ArrayList<Edge>> graph;
PriorityQueue<Edge> pQ;
Prim(int v){
minimumCost = 0;
ch = new int[v+1];
graph = new ArrayList<>();
pQ = new PriorityQueue<>();
for(int i=0; i<=v; i++){
graph.add(new ArrayList<Edge>());
}
}
public void spanningTree() {
pQ.offer(new Edge(1,0));
while(!pQ.isEmpty()){
Edge tmp = pQ.poll();
int ev = tmp.vex1;
if(ch[ev] == 0){
ch[ev] = 1;
minimumCost += tmp.cost;
for(Edge ob : graph.get(ev)){
if(ch[ob.vex1]==0) pQ.offer(new Edge(ob.vex1, ob.cost));
}
}
}
}
}
class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int v = Integer.parseInt(st.nextToken());
int n = Integer.parseInt(st.nextToken());
Kruskal kruskal = new Kruskal(v);
Prim prim = new Prim(v);
for(int i = 0; i < n; i++){
st = new StringTokenizer(br.readLine());
// a정점
int a = Integer.parseInt(st.nextToken());
// b정점
int b = Integer.parseInt(st.nextToken());
// 가중치
int c = Integer.parseInt(st.nextToken());
kruskal.list.add(new Edge(a, b, c));
prim.graph.get(a).add(new Edge(b, c));
prim.graph.get(b).add(new Edge(a, c));
}
Collections.sort(kruskal.list);
kruskal.spanningTree();
prim.spanningTree();
System.out.println(kruskal.minimumCost);
//System.out.println(prim.minimumCost);
}
}'Algorithm > 알고리즘 개념' 카테고리의 다른 글
| [알고리즘] 삽입 정렬(insertion sort) (0) | 2023.05.10 |
|---|---|
| [알고리즘] 버블 정렬(bubble sort) (0) | 2023.05.10 |
| [알고리즘] Union-Find Algorithm (유니온 파인드 알고리즘) (0) | 2023.04.04 |
| [알고리즘] Dijkstra Algorithm (다익스트라 알고리즘) (0) | 2023.04.04 |
| [알고리즘] Greedy Algorithm(탐욕 알고리즘) (0) | 2023.04.03 |
