다익스트라 알고리즘이란?
💡다익스트라 알고리즘: 데이크스트라 또는 다익스트라 알고리즘이라 불리는 이 알고리즘은 음의 가중치가 없는 그래프에서 최단 경로 및 최단 거리를 찾는 알고리즘이다.
매번 최단 경로의 정점을 선택하기 때문에 그리디 알고리즘 기법을 활용한 예라고 볼 수 있다. 중요한 점은 음의 가중치가 없을 때만 사용이 가능하다는 점이다. 인접행렬을 사용하는 경우 O(n^2)의 시간복잡도를 가지지만, 우선순위 큐(=힙 트리)등을 이용한다면 O((v+e)logV)(V는 정점의 개수, E는 한 정점의 주변노드)의 시간복잡도를 가진다.
음의 가중치를 가지는 간선이 있으며, 가중치 합이 음인 사이클이 존재하지 않는 경우 벨만-포드 알고리즘을 사용할 수 있다.
가능한 적은 비용으로 가장 빠르게 해답에 도달하는 경로를 찾아내는 대부분의 문제에서 활용할 수 있다.
다익스트라 알고리즘 예제
아래의 가중치 방향그래프에서 1번 정점에서 모든 정점으로의 최소 거리비용을 출력하는 프로그램을 작성하세요. (경로가 없으면 Impossible를 출력한다.)
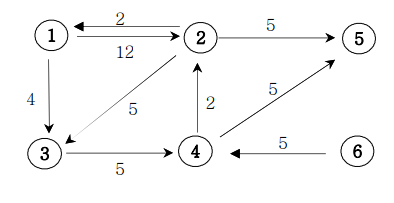
입력 예제
6 9
1 2 12 // 1번 정점에서 2번정점으로 가는데 12의 비용이 든다.
1 3 4
2 1 2
2 3 5
2 5 5
3 4 5
4 2 2
4 5 5
6 4 5출력 예제
2 : 11
3 : 4
4 : 9
5 : 14
6 : impossible
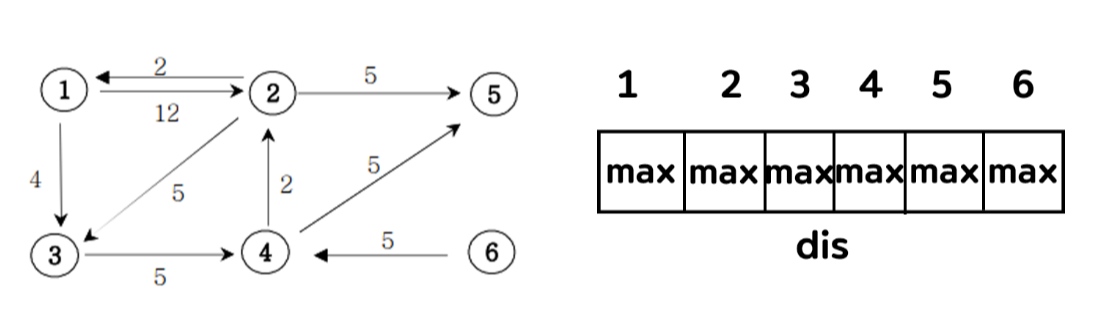
1) 정점의 개수만큼 이루어진 dis 배열을 만든다. 이때 Integer Max 값으로 배열을 채워준다.
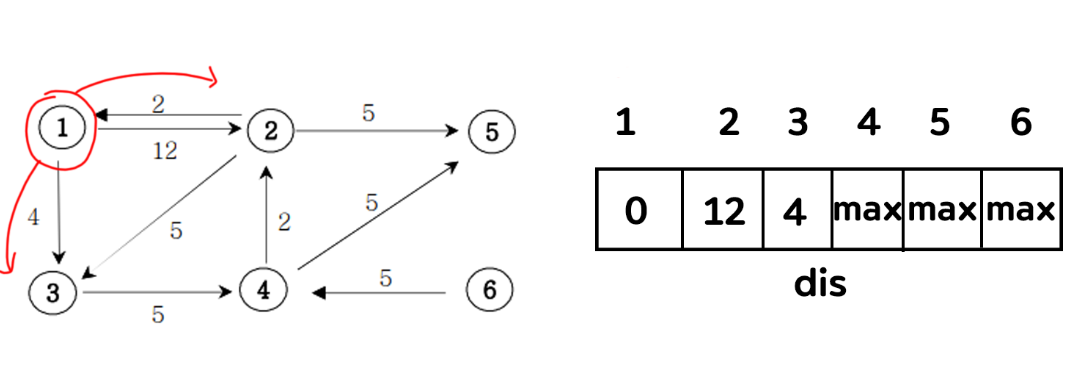
2) 1번에서 인접한 노드들을 살펴보자 각 2와 3이 존재한다. dis배열에 담긴 값과 비용을 비교하여 작은 값을 넣어준다. 그렇게 되면 배열에 각각 12와 4가 들어가게 될 것이다. (1인덱스 값 더하기 가중치로 계산)
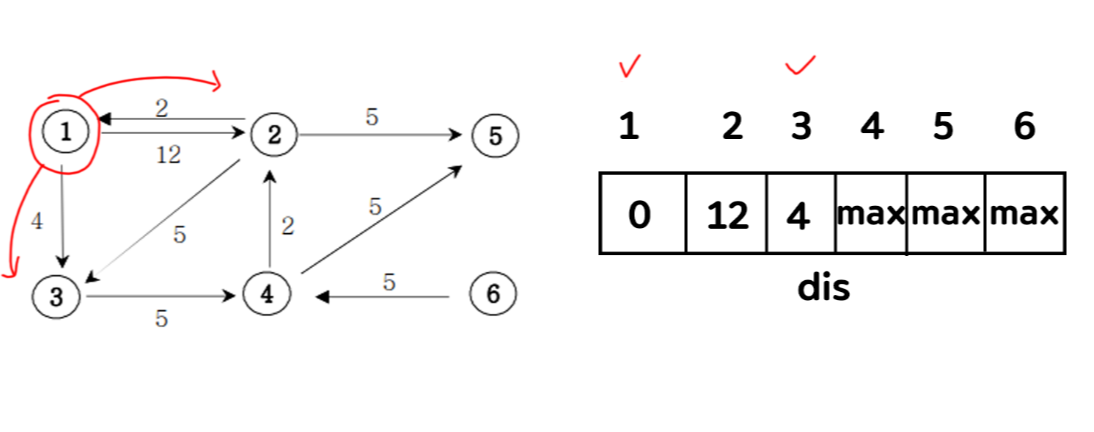
3) 이때 1은 이미 방문됐다 표시를 하고, 그 다음 방문하지 않은 2번 정점과 3번 정점을 비교한다. 이때 3번 정점의 값이 더 작으므로 방문 표시를 해주며 3에서부터 다시 뻗어나간다. 음의 가중치는 존재하지 않는다는 전제에 사용하는 다익스트라 알고리즘이기 때문에 4보다 더 작은 값이 생길리가 없다.
4) 같은 방식으로 다음 노드도 값을 구한다. 정점3과 인접한 노드는 4밖에 없다. 이때 4의 값은 3의 정점에서 시작했으니 인덱스 3번째 배열의 값과 가중치를 더해 9를 넣어준다. (4 + 5). 더 작은 값을 구할 수 없으니 정점 4를 체크해준다.
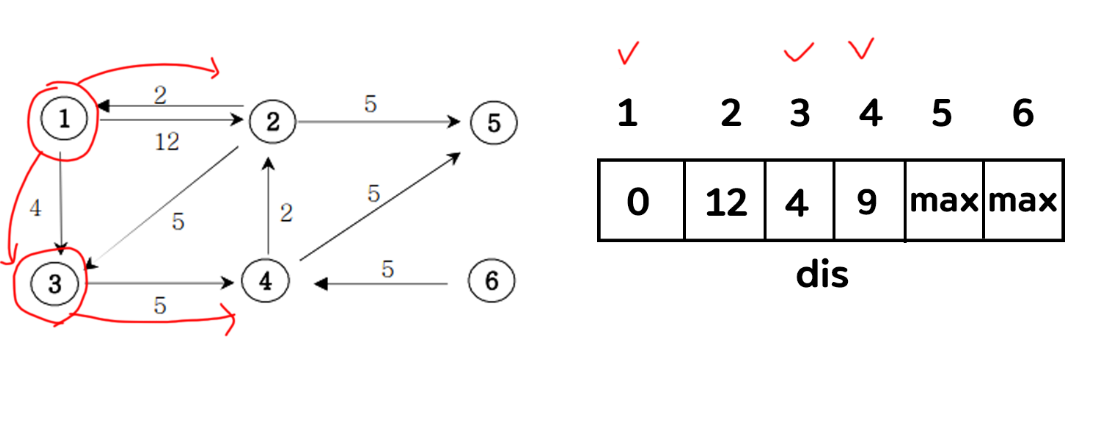
5) 4번에서는 2번과 5번에 접근 할 수 있다. 이때 2로 갈 때의 값은 9 + 2 이므로 11이 된다. 원래 배열에 들어간 값보다 11이 더 작기 때문에 11로 바꿔준다. 5로 이동했을 때의 값은 14이다. 14와 11을 비교했을 때 11이 더 작기 때문에 2번 정점을 체크해준다.
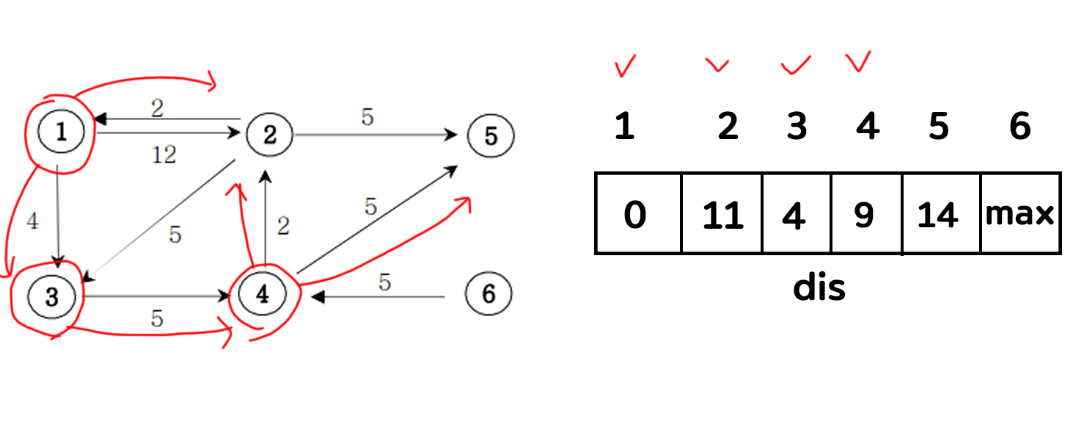
6) 2에서 뻗어나갈 수 있는 정점은 3번과 5번이다. 3번으로 갔을 때 16이 되는데, 3번에 들어있는 값 4가 더 작으니 아무일도 생기지 않는다. 5번 정점으로 갔을 때도 마찬가지다. 11 + 5 = 16과 원래 있던 값 14를 비교했을 때 14가 더 작기 때문에 아무일도 생기지 않는다. 14와 16을 다시 비교하면 14가 더 작으니 5번을 체크해준다.
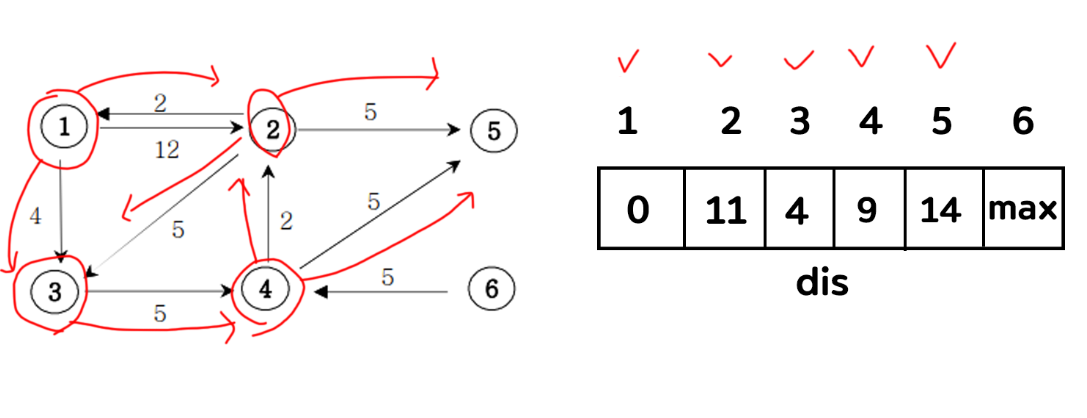
7) 완성된 dis 배열이 1에서부터 갈 수 있는 모든 정점의 최소 거리이다.
완성 예제
import java.util.*;
class Edge implements Comparable<Edge>{
public int vex; // 정점
public int cost; // 비용
Edge(int vex, int cost) {
this.vex = vex;
this.cost = cost;
}
// 비용 중심으로 우선순위가 정해져야함. 우선순위 큐에서 활용하기 위함
@Override
public int compareTo(Edge ob){
return this.cost-ob.cost;
}
}
class Main {
static int n, m;
static ArrayList<ArrayList<Edge>> graph;
static int[] dis;
public void solution(int v){
// 우선순위 큐이기 때문에 비용이 적은 것부터 검사하게 됨
PriorityQueue<Edge> pQ = new PriorityQueue<>();
pQ.offer(new Edge(v, 0));
dis[v]=0;
while(!pQ.isEmpty()){
Edge tmp=pQ.poll();
int now=tmp.vex;
int nowCost=tmp.cost;
if(nowCost>dis[now]) continue;
for(Edge ob : graph.get(now)){
if(dis[ob.vex]>nowCost+ob.cost){
dis[ob.vex]=nowCost+ob.cost;
pQ.offer(new Edge(ob.vex, nowCost+ob.cost));
}
}
}
}
public static void main(String[] args){
Main T = new Main();
Scanner kb = new Scanner(System.in);
n=kb.nextInt();
m=kb.nextInt();
graph = new ArrayList<ArrayList<Edge>>();
for(int i=0; i<=n; i++){
graph.add(new ArrayList<Edge>());
}
dis=new int[n+1];
Arrays.fill(dis, Integer.MAX_VALUE);
for(int i=0; i<m; i++){
int a=kb.nextInt();
int b=kb.nextInt();
int c=kb.nextInt();
graph.get(a).add(new Edge(b, c));
}
T.solution(1);
for(int i=2; i<=n; i++){
if(dis[i]!=Integer.MAX_VALUE) System.out.println(i+" : "+dis[i]);
else System.out.println(i+" : impossible");
}
}
}
Reference
자바 알고리즘 문제풀이 코테대비-인프런
'Algorithm > 알고리즘 개념' 카테고리의 다른 글
| [알고리즘] 최소 신장 트리 - Prim, Kruskal Algorithm(프림, 크루스칼 알고리즘) (0) | 2023.04.05 |
|---|---|
| [알고리즘] Union-Find Algorithm (유니온 파인드 알고리즘) (0) | 2023.04.04 |
| [알고리즘] Greedy Algorithm(탐욕 알고리즘) (0) | 2023.04.03 |
| [알고리즘] 02. DFS와 BFS (1) | 2023.03.27 |
| [알고리즘] 01. 비트마스크(Bit mask) (2) | 2023.02.27 |
