트리 란?
💡트리: 단반향 그래프의 한 구조로, 하나의 뿌리로부터 가지가 사방으로 뻗는 형태가 나무와 닮았다고 해서 트리라 부르는 자료구조이다. 데이터가 바로 아래에 있는 하나 이상의 데이터에 무방향으로 연결된 계층적 자료구조. 비선형구조이다.
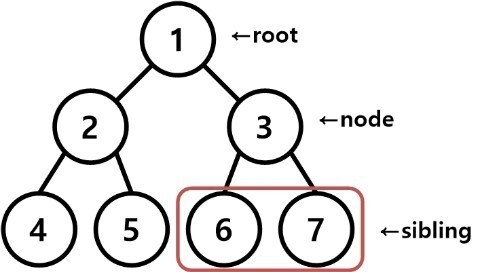
트리 구조는 루트(root)라는 하나의 꼭짓점 데이터를 시작으로 여러 개의 데이터를 간선(edge)으로 연결한다. 각 데이터를 노드(node)라 부르며, 두 개의 노드가 상하 계층으로 연결되면 부모/자식 관계를 가지게 된다.
위 그림에서 1이 2와 3의 부모 노드이며, 2와 3은 1의 자식노드이다. 자식이 없는 노드는 나무의 잎과 같다고 하여 리프 노드(Leaf Node)라 부른다.
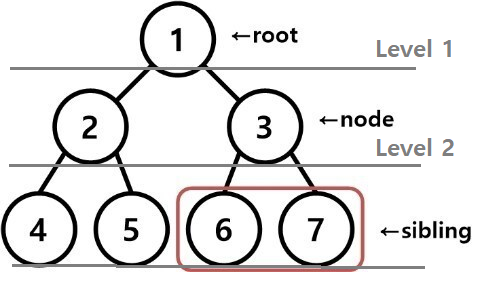
Tree는 깊이와 높이, 레벨을 측정할 수 있다.
깊이(depth): 루트로부터 하위 계층의 특정 노드까지의 깊이를 말한다.
ex) 1의 깊이는 0, 2와 3의깊이는 1
레벨(Level): 같은 깊이를 가지고 있는 노드를 묶어서 말한다. 같은 레벨에 놓여있는 노드를 형제 노드(Slibling Node)라 부른다.
ex) 1의 레벨은 1, 2와 3의 레벨은 2
높이(Height): 리프 노드를 기준으로 루트까지의 높이를 말한다.
ex) 1의 높이는 2, 2와 3의 높이는 1, 4와 5, 6과 7의 높이는 0
이진 트리
이진 트리(Binary Tree): 자식 노드가 최대 두개인 노드들로 구성된 트리. 이 두개의 자식 노드는 왼쪽 자식 노드, 오른쪽 자식 노드로 나눌 수 있다.
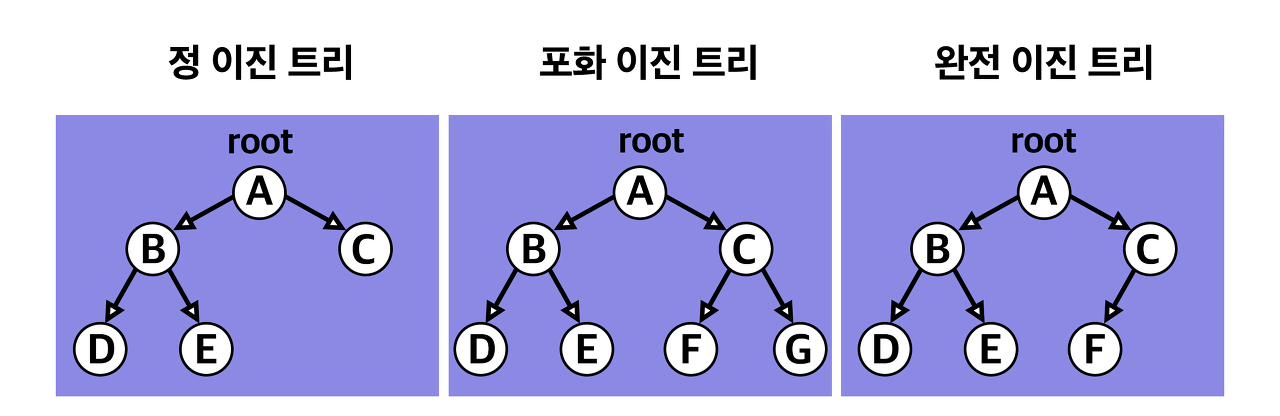
정 이진 트리(Full binary tree): 각 노드가 0개 혹은 2개의 자식 노드를 갖는다.
포화 이진 트리(Perfect binary tree): 정 이진 트리이면서 완전 이진 트리인 경우이다. 모든 리프 노드의 레벨이 동일하고, 모든 레벨이 가득 채워져 있는 트리이다.
완전 이진 트리(Complete binary tree): 마지막 레벨을 제외한 모든 노드가 가득 차 있어야 하고, 마지막 레벨의 노드는 전부 차 있지 않아도 되지만, 왼쪽은 채워져 있어야 한다.
트리 순회
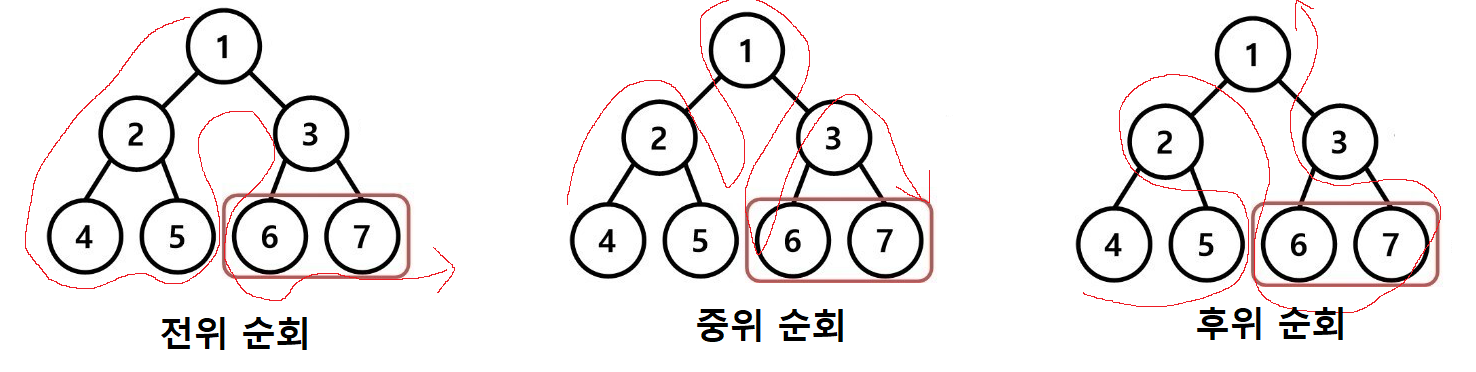
순회 방법에는 전위 순회, 중위 순회, 후위 순회 3가지 방법이 있다. 기준을 루트로 잡고 이름 그대로 순회하는 방식이며, 이 원리를 안다면 트리 순회에 대한 이해가 어렵지 않을 것이다.
전위 순회:
현재 자기 자신(루트) 노드를 제일 먼저 순회하고 Left -> Right 순으로 순회하는 방법이다.
그림의 루트는 1, 그렇기 때문에 1부터 순회하고 부모 노드가 2 자식노드가 4,5 인 서브 트리를 살펴보자. 서브 트리의 루트는 2, 때문에 1을 순회한 다음 2를 순회한다. 이 원리를 따라 트리 전체를 전위 순회 방법으로 순회한다면, 1->2->4->5->3->6->7 순서로 순회할 것이다.
중위 순회:
현재 자기 자신(루트) 노드를 중간에 순회하는 방법으로 Left -> Loot -> Right 순으로 순회하는 방법이다.
4->2->5->1->6->3->7
후위 순회:
현재 자기 자신(루트) 노드를 마지막에 순회하는 방법으로 Left -> Right -> Loot 순으로 순회하는 방법이다.
4->5->2->6->7->3->1
import lombok.Getter;
import lombok.Setter;
import java.util.ArrayList;
@Getter @Setter
public class Node {
private int data;
private Node left;
private Node right;
/* 생성자 */
public Node(int data) {
this.setData(data);
this.setLeft(null);
this.setRight(null);
}
}
class binarySearchTree {
public Node root;
public binarySearchTree(){
root = null;
}
public void insert(int data) {
Node newNode = new Node(data);
if (root == null) {
root = newNode;
return;
}
if(root.data == data) return;
Node currentNode = root;
Node parentNode = null;
while (true) {
parentNode = currentNode;
if (data < currentNode.getData()) {
currentNode = currentNode.getLeft();
if (currentNode == null) {
parentNode.setLeft(newNode);
return;
}else if(currentNode.data == newNode.data) return;
} else {
currentNode = currentNode.getRight();
if (currentNode == null) {
parentNode.setRight(newNode);
return;
}else if(currentNode.data == newNode.data) return;
}
}
}
public boolean find(int data) {
Node currentNode = root;
while (currentNode != null) {
if (currentNode.data == data) {
return true;
}
if (currentNode.data > data) {
currentNode = currentNode.left;
}else {
currentNode = currentNode.right;
}
}
return false;
}
public ArrayList<Integer> preorderTree(Node root, int depth, ArrayList<Integer> list) { //전위 순회
if (root != null) {
list.add(root.getData());
preorderTree(root.getLeft(), depth + 1, list);
preorderTree(root.getRight(), depth + 1, list);
}
return list;
}
public ArrayList<Integer> inorderTree(Node root, int depth, ArrayList<Integer> list) { //중위 순회
if (root != null) {
inorderTree(root.getLeft(), depth + 1, list);
list.add(root.getData());
inorderTree(root.getRight(), depth + 1, list);
}
return list;
}
public ArrayList<Integer> postorderTree(Node root, int depth, ArrayList<Integer> list) { //후위 순회
if (root != null) {
postorderTree(root.getLeft(), depth + 1, list);
postorderTree(root.getRight(), depth + 1, list);
list.add(root.getData());
}
return list;
}
// 레벨 순회
public ArrayList<Integer> BFS(Node focusNode){
if(focusNode == null){
return null;
}
ArrayList<Integer> result = new ArrayList<>();
Queue<Node> queue = new LinkedList<>();
queue.add(focusNode);
while (!queue.isEmpty()){
int size = queue.size();
for (int i = 0; i < size; i++) {
Node poll = queue.poll();
if(poll.getLeft() !=null){
queue.add(poll.getLeft());
}
if(poll.getRight() !=null){
queue.add(poll.getRight());
}
result.add(poll.getData());
}
}
return result;
}
}코드의 전제조건은
왼쪽노드가 오른쪽 노드보다 더 작아야하며, 중복되는 값은 없어야 한다.
위 소스의 전위, 중위, 후위 순회는 DFS(깊이 우선 탐색)이며, 레벨 순회가 곧 BFS(넓이 우선 탐색)이다.
DFS와 BFS를 블로깅 하기 전 예습 단계로 그래프와 트리를 블로깅해두고 간다 ~
'Algorithm > 자료구조 개념' 카테고리의 다른 글
| [자료구조] 04. 배열(Array) (0) | 2024.01.17 |
|---|---|
| [자료구조] 자바의 자료구조 개념 정리 - 2 (1) | 2024.01.10 |
| [자료구조] 자바의 자료구조(Collection) - 1 (2) | 2024.01.04 |
| [자료구조] 03. 해시 테이블 (0) | 2023.04.05 |
| [자료구조] 01. 그래프 (0) | 2023.03.27 |
트리 란?
💡트리: 단반향 그래프의 한 구조로, 하나의 뿌리로부터 가지가 사방으로 뻗는 형태가 나무와 닮았다고 해서 트리라 부르는 자료구조이다. 데이터가 바로 아래에 있는 하나 이상의 데이터에 무방향으로 연결된 계층적 자료구조. 비선형구조이다.

트리 구조는 루트(root)라는 하나의 꼭짓점 데이터를 시작으로 여러 개의 데이터를 간선(edge)으로 연결한다. 각 데이터를 노드(node)라 부르며, 두 개의 노드가 상하 계층으로 연결되면 부모/자식 관계를 가지게 된다.
위 그림에서 1이 2와 3의 부모 노드이며, 2와 3은 1의 자식노드이다. 자식이 없는 노드는 나무의 잎과 같다고 하여 리프 노드(Leaf Node)라 부른다.

Tree는 깊이와 높이, 레벨을 측정할 수 있다.
깊이(depth): 루트로부터 하위 계층의 특정 노드까지의 깊이를 말한다.
ex) 1의 깊이는 0, 2와 3의깊이는 1
레벨(Level): 같은 깊이를 가지고 있는 노드를 묶어서 말한다. 같은 레벨에 놓여있는 노드를 형제 노드(Slibling Node)라 부른다.
ex) 1의 레벨은 1, 2와 3의 레벨은 2
높이(Height): 리프 노드를 기준으로 루트까지의 높이를 말한다.
ex) 1의 높이는 2, 2와 3의 높이는 1, 4와 5, 6과 7의 높이는 0
이진 트리

이진 트리(Binary Tree): 자식 노드가 최대 두개인 노드들로 구성된 트리. 이 두개의 자식 노드는 왼쪽 자식 노드, 오른쪽 자식 노드로 나눌 수 있다.
정 이진 트리(Full binary tree): 각 노드가 0개 혹은 2개의 자식 노드를 갖는다.
포화 이진 트리(Perfect binary tree): 정 이진 트리이면서 완전 이진 트리인 경우이다. 모든 리프 노드의 레벨이 동일하고, 모든 레벨이 가득 채워져 있는 트리이다.
완전 이진 트리(Complete binary tree): 마지막 레벨을 제외한 모든 노드가 가득 차 있어야 하고, 마지막 레벨의 노드는 전부 차 있지 않아도 되지만, 왼쪽은 채워져 있어야 한다.
트리 순회

순회 방법에는 전위 순회, 중위 순회, 후위 순회 3가지 방법이 있다. 기준을 루트로 잡고 이름 그대로 순회하는 방식이며, 이 원리를 안다면 트리 순회에 대한 이해가 어렵지 않을 것이다.
전위 순회:
현재 자기 자신(루트) 노드를 제일 먼저 순회하고 Left -> Right 순으로 순회하는 방법이다.
그림의 루트는 1, 그렇기 때문에 1부터 순회하고 부모 노드가 2 자식노드가 4,5 인 서브 트리를 살펴보자. 서브 트리의 루트는 2, 때문에 1을 순회한 다음 2를 순회한다. 이 원리를 따라 트리 전체를 전위 순회 방법으로 순회한다면, 1->2->4->5->3->6->7 순서로 순회할 것이다.
중위 순회:
현재 자기 자신(루트) 노드를 중간에 순회하는 방법으로 Left -> Loot -> Right 순으로 순회하는 방법이다.
4->2->5->1->6->3->7
후위 순회:
현재 자기 자신(루트) 노드를 마지막에 순회하는 방법으로 Left -> Right -> Loot 순으로 순회하는 방법이다.
4->5->2->6->7->3->1
import lombok.Getter;
import lombok.Setter;
import java.util.ArrayList;
@Getter @Setter
public class Node {
private int data;
private Node left;
private Node right;
/* 생성자 */
public Node(int data) {
this.setData(data);
this.setLeft(null);
this.setRight(null);
}
}
class binarySearchTree {
public Node root;
public binarySearchTree(){
root = null;
}
public void insert(int data) {
Node newNode = new Node(data);
if (root == null) {
root = newNode;
return;
}
if(root.data == data) return;
Node currentNode = root;
Node parentNode = null;
while (true) {
parentNode = currentNode;
if (data < currentNode.getData()) {
currentNode = currentNode.getLeft();
if (currentNode == null) {
parentNode.setLeft(newNode);
return;
}else if(currentNode.data == newNode.data) return;
} else {
currentNode = currentNode.getRight();
if (currentNode == null) {
parentNode.setRight(newNode);
return;
}else if(currentNode.data == newNode.data) return;
}
}
}
public boolean find(int data) {
Node currentNode = root;
while (currentNode != null) {
if (currentNode.data == data) {
return true;
}
if (currentNode.data > data) {
currentNode = currentNode.left;
}else {
currentNode = currentNode.right;
}
}
return false;
}
public ArrayList<Integer> preorderTree(Node root, int depth, ArrayList<Integer> list) { //전위 순회
if (root != null) {
list.add(root.getData());
preorderTree(root.getLeft(), depth + 1, list);
preorderTree(root.getRight(), depth + 1, list);
}
return list;
}
public ArrayList<Integer> inorderTree(Node root, int depth, ArrayList<Integer> list) { //중위 순회
if (root != null) {
inorderTree(root.getLeft(), depth + 1, list);
list.add(root.getData());
inorderTree(root.getRight(), depth + 1, list);
}
return list;
}
public ArrayList<Integer> postorderTree(Node root, int depth, ArrayList<Integer> list) { //후위 순회
if (root != null) {
postorderTree(root.getLeft(), depth + 1, list);
postorderTree(root.getRight(), depth + 1, list);
list.add(root.getData());
}
return list;
}
// 레벨 순회
public ArrayList<Integer> BFS(Node focusNode){
if(focusNode == null){
return null;
}
ArrayList<Integer> result = new ArrayList<>();
Queue<Node> queue = new LinkedList<>();
queue.add(focusNode);
while (!queue.isEmpty()){
int size = queue.size();
for (int i = 0; i < size; i++) {
Node poll = queue.poll();
if(poll.getLeft() !=null){
queue.add(poll.getLeft());
}
if(poll.getRight() !=null){
queue.add(poll.getRight());
}
result.add(poll.getData());
}
}
return result;
}
}코드의 전제조건은
왼쪽노드가 오른쪽 노드보다 더 작아야하며, 중복되는 값은 없어야 한다.
위 소스의 전위, 중위, 후위 순회는 DFS(깊이 우선 탐색)이며, 레벨 순회가 곧 BFS(넓이 우선 탐색)이다.
DFS와 BFS를 블로깅 하기 전 예습 단계로 그래프와 트리를 블로깅해두고 간다 ~
'Algorithm > 자료구조 개념' 카테고리의 다른 글
| [자료구조] 04. 배열(Array) (0) | 2024.01.17 |
|---|---|
| [자료구조] 자바의 자료구조 개념 정리 - 2 (1) | 2024.01.10 |
| [자료구조] 자바의 자료구조(Collection) - 1 (2) | 2024.01.04 |
| [자료구조] 03. 해시 테이블 (0) | 2023.04.05 |
| [자료구조] 01. 그래프 (0) | 2023.03.27 |
