💡비트마스크: 알고리즘보다는 기법이나 테크닉에 가깝다. 자료구조를 사용해야하는 상황에서 이진수를 이용하여 빠르게 연산하는 기법이라 말할 수 있다.
비트 마스크를 알기 전에 비트가 무엇인지 부터 알아야 한다.
비트(Bit)
💡비트(Binary Digit, Bit): 데이터들을 나타내는 최소 단위, 이진수로 표현한다.(0과 1)
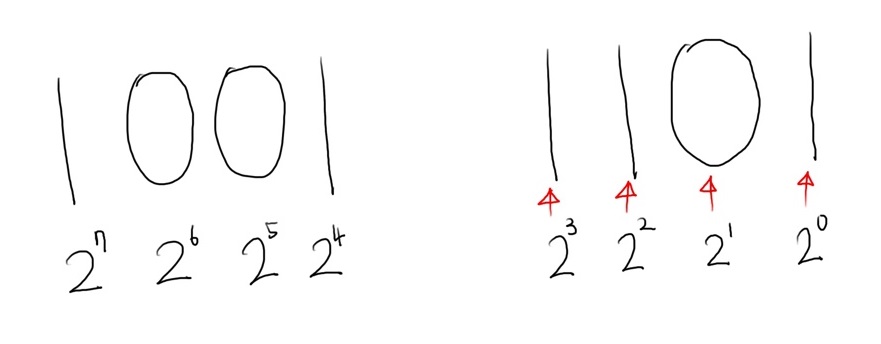
비트 연산자
| 구분 | 연산자 | 의미 | 설명 | 예시(a=1001, b= 1100) |
| 비트연산자 | & | 비트 단위 AND | 양쪽 비트가 모두 1이면 결과도 1이고 나머지는 0을 반환한다. | a&b = 1000 |
| | | 비트 단위 OR | 양쪽 비트 중 하나라도 1이면 1을 반환, 나머지는 0을 반환한다. | a|b = 1101 | |
| ^ | XOR(배타적 OR) | 양쪽 비트가 서로 다르면 1, 같은면 0을 반환한다. | a^b = 1010 | |
| ~ | NOT | 1을 0으로, 0을 1로 반환한다. | ~a = 110 | |
| 비트 이동연산자 | << | a를 왼쪽으로 b비트 만큼 이동한다.(빈자리는 0으로 채워짐) | a << 2 -> 100100 2^2만큼 곱하기 |
|
| >> | a를 오른쪽으로 b비트만큼 이동한다.(왼쪽 빈자리는 최상위 부호비트와 같은 값으로 채워진다.) | |||
| >>> | a를 오른쪽으로 b비트만큼 이동한다.(빈자리는 0으로 채워) | a >>2 -> 10 2^2만큼 나눗셈 |
||
비트 마스크(Bit mask)
그럼 이 비트를 가지고 어떻게 자료구조처럼 사용할 수가 있나?
비트는 1과0으로 구성되어 있어 집합을 쉽게 표현할 수 있다.
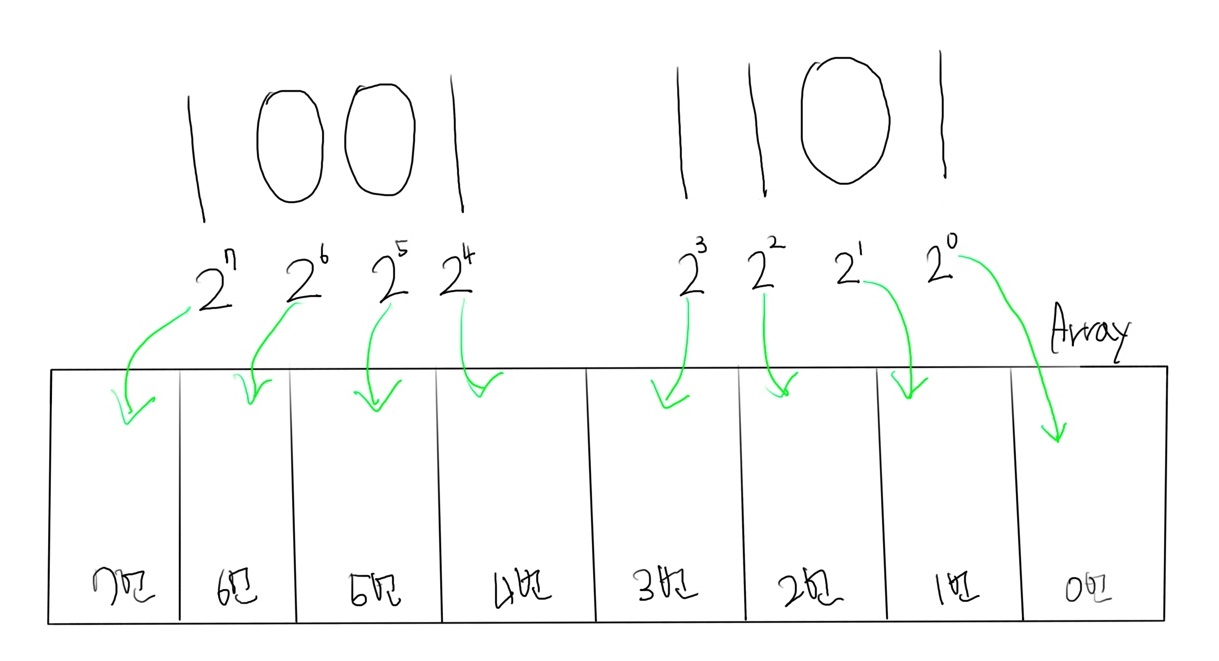
위의 사진을 보면 이해하기가 쉬울 것이다.
157로 나타냈던 숫자를 비트 마스킹 기법을 사용한다고 하면, {1, 3, 4, 5, 8} 5개의 요소를 가지고 있는 배열처럼 볼 수 있다. 1을 true로 0을 false로 본다는 것!
그런데 왜? 편한 컬렉션이나 배열을 두고 이런 기법을 사용할까.

내가 비트 마스크에 대해 알아보게된 계기이다. 백준 문제를 풀었는데 정답이긴 했으나, 메모리와 시간면에서 비효율적이라는 생각이 들어 답지를 찾아봤다.
나는 ArrayList로 풀었는데, 몇몇 사람들은 비트 마스킹 기법을 사용해서 문제를 풀었더라.
이처럼 비트 마스크 기법을 사용하면 시간복잡도 O(1)으로 시간을 더 절약할 수 있고, list가 아닌 정수로 표현하다보니 메모리도 더 적게 사용할 수 있다.
- 수행 시간이 더 빠르다
- 메모리 측면에서 효율적이다.
응용
| 연산 | 코드 | 설명 |
| 공집합, 꽉찬 집합 | int A = 0, int A = (1 << N) -1 | 0으로 채운다. N만큼 비트를 1로 채운다. |
| 원소 추가 | A |= (1 << N), int k = A | (1<<N) | N번째에 비트 1로 바꾸기, 비트 켜기 |
| 원소 삭제 | A &= ~(1 << N), int k = A & ~(1<<N) | N번째에 비트 0으로 바꾸기, 비트 끄기 |
| 원소 확인 | int k = A & (1 << N) | N번째 비트 확인 |
| 원소 포함 여부 확인 | if( (A&(1<<N)) == (1<<N) ) | A의 집합에서 N번째 원소가 있는지 확인 |
| 원소 토글 | A ^= (1 << N), int k = A^(1 << N) | N번째 비트 변경, 1은 0으로 0은 1로 |
| 두 집합 연산 | A | B, A & B, A & -B, A ^ B | 각각 합집합, 교집합, 차집합, 하나에만 켜진 비트의 집합 |
| 집합 내 원소 개수 | Integer.bitCount(A) | A 집합의 1로 된 비트 수 반환 |
| 왼쪽 원소 모두 0 | A &= ( (1<<N) - 1 ) | N번째 기준으로 왼쪽 모두 0으로 변경 |
| 오른쪽 원소 모두 0 | A &= (-1 << N) | N번째 기준으로 오른쪽 모두 0으로 변경 |
| 부분집합 | for(int subset = A; subset > 0; subset = (( subset -1 ) & A) ) | A 집합에서 나올 수 있는 부분집합 |
| 최소 원소 반환 | int min = A & (-A) | A집합에서 1로된 비트 중 최소 비트 반환 |
| 최소 원소 지우기 | A &= ( A -1 ) | A집합에서 켜져있는 비트 중 최소 비트 0으로 변경 |
Reference
'Algorithm > 알고리즘 개념' 카테고리의 다른 글
| [알고리즘] 최소 신장 트리 - Prim, Kruskal Algorithm(프림, 크루스칼 알고리즘) (0) | 2023.04.05 |
|---|---|
| [알고리즘] Union-Find Algorithm (유니온 파인드 알고리즘) (0) | 2023.04.04 |
| [알고리즘] Dijkstra Algorithm (다익스트라 알고리즘) (0) | 2023.04.04 |
| [알고리즘] Greedy Algorithm(탐욕 알고리즘) (0) | 2023.04.03 |
| [알고리즘] 02. DFS와 BFS (1) | 2023.03.27 |
💡비트마스크: 알고리즘보다는 기법이나 테크닉에 가깝다. 자료구조를 사용해야하는 상황에서 이진수를 이용하여 빠르게 연산하는 기법이라 말할 수 있다.
비트 마스크를 알기 전에 비트가 무엇인지 부터 알아야 한다.
비트(Bit)
💡비트(Binary Digit, Bit): 데이터들을 나타내는 최소 단위, 이진수로 표현한다.(0과 1)
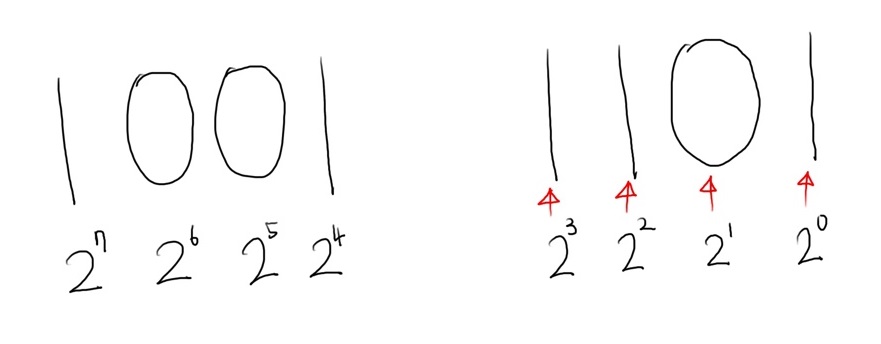
비트 연산자
| 구분 | 연산자 | 의미 | 설명 | 예시(a=1001, b= 1100) |
| 비트연산자 | & | 비트 단위 AND | 양쪽 비트가 모두 1이면 결과도 1이고 나머지는 0을 반환한다. | a&b = 1000 |
| | | 비트 단위 OR | 양쪽 비트 중 하나라도 1이면 1을 반환, 나머지는 0을 반환한다. | a|b = 1101 | |
| ^ | XOR(배타적 OR) | 양쪽 비트가 서로 다르면 1, 같은면 0을 반환한다. | a^b = 1010 | |
| ~ | NOT | 1을 0으로, 0을 1로 반환한다. | ~a = 110 | |
| 비트 이동연산자 | << | a를 왼쪽으로 b비트 만큼 이동한다.(빈자리는 0으로 채워짐) | a << 2 -> 100100 2^2만큼 곱하기 |
|
| >> | a를 오른쪽으로 b비트만큼 이동한다.(왼쪽 빈자리는 최상위 부호비트와 같은 값으로 채워진다.) | |||
| >>> | a를 오른쪽으로 b비트만큼 이동한다.(빈자리는 0으로 채워) | a >>2 -> 10 2^2만큼 나눗셈 |
||
비트 마스크(Bit mask)
그럼 이 비트를 가지고 어떻게 자료구조처럼 사용할 수가 있나?
비트는 1과0으로 구성되어 있어 집합을 쉽게 표현할 수 있다.

위의 사진을 보면 이해하기가 쉬울 것이다.
157로 나타냈던 숫자를 비트 마스킹 기법을 사용한다고 하면, {1, 3, 4, 5, 8} 5개의 요소를 가지고 있는 배열처럼 볼 수 있다. 1을 true로 0을 false로 본다는 것!
그런데 왜? 편한 컬렉션이나 배열을 두고 이런 기법을 사용할까.

내가 비트 마스크에 대해 알아보게된 계기이다. 백준 문제를 풀었는데 정답이긴 했으나, 메모리와 시간면에서 비효율적이라는 생각이 들어 답지를 찾아봤다.
나는 ArrayList로 풀었는데, 몇몇 사람들은 비트 마스킹 기법을 사용해서 문제를 풀었더라.
이처럼 비트 마스크 기법을 사용하면 시간복잡도 O(1)으로 시간을 더 절약할 수 있고, list가 아닌 정수로 표현하다보니 메모리도 더 적게 사용할 수 있다.
- 수행 시간이 더 빠르다
- 메모리 측면에서 효율적이다.
응용
| 연산 | 코드 | 설명 |
| 공집합, 꽉찬 집합 | int A = 0, int A = (1 << N) -1 | 0으로 채운다. N만큼 비트를 1로 채운다. |
| 원소 추가 | A |= (1 << N), int k = A | (1<<N) | N번째에 비트 1로 바꾸기, 비트 켜기 |
| 원소 삭제 | A &= ~(1 << N), int k = A & ~(1<<N) | N번째에 비트 0으로 바꾸기, 비트 끄기 |
| 원소 확인 | int k = A & (1 << N) | N번째 비트 확인 |
| 원소 포함 여부 확인 | if( (A&(1<<N)) == (1<<N) ) | A의 집합에서 N번째 원소가 있는지 확인 |
| 원소 토글 | A ^= (1 << N), int k = A^(1 << N) | N번째 비트 변경, 1은 0으로 0은 1로 |
| 두 집합 연산 | A | B, A & B, A & -B, A ^ B | 각각 합집합, 교집합, 차집합, 하나에만 켜진 비트의 집합 |
| 집합 내 원소 개수 | Integer.bitCount(A) | A 집합의 1로 된 비트 수 반환 |
| 왼쪽 원소 모두 0 | A &= ( (1<<N) - 1 ) | N번째 기준으로 왼쪽 모두 0으로 변경 |
| 오른쪽 원소 모두 0 | A &= (-1 << N) | N번째 기준으로 오른쪽 모두 0으로 변경 |
| 부분집합 | for(int subset = A; subset > 0; subset = (( subset -1 ) & A) ) | A 집합에서 나올 수 있는 부분집합 |
| 최소 원소 반환 | int min = A & (-A) | A집합에서 1로된 비트 중 최소 비트 반환 |
| 최소 원소 지우기 | A &= ( A -1 ) | A집합에서 켜져있는 비트 중 최소 비트 0으로 변경 |
Reference
'Algorithm > 알고리즘 개념' 카테고리의 다른 글
| [알고리즘] 최소 신장 트리 - Prim, Kruskal Algorithm(프림, 크루스칼 알고리즘) (0) | 2023.04.05 |
|---|---|
| [알고리즘] Union-Find Algorithm (유니온 파인드 알고리즘) (0) | 2023.04.04 |
| [알고리즘] Dijkstra Algorithm (다익스트라 알고리즘) (0) | 2023.04.04 |
| [알고리즘] Greedy Algorithm(탐욕 알고리즘) (0) | 2023.04.03 |
| [알고리즘] 02. DFS와 BFS (1) | 2023.03.27 |
