DFS와 BFS를 알기전에 트리와 그래프가 무엇인지 부터 알아야 한다.
https://memodayoungee.tistory.com/85
[자료구조] 02. Tree
트리 란? 💡트리: 단반향 그래프의 한 구조로, 하나의 뿌리로부터 가지가 사방으로 뻗는 형태가 나무와 닮았다고 해서 트리라 부르는 자료구조이다. 데이터가 바로 아래에 있는 하나 이상의 데
memodayoungee.tistory.com
https://memodayoungee.tistory.com/84
[자료구조] 01. 그래프
DFS, BFS에 대한 이야기를 하려다 어쩌다보니 그래프를 작성하게 되었다.. 안좋을 점은 없으니까.. 블로그에 남겨두고 간다... 그래프 란? 💡그래프: 여러 개의 점들이 서로 복잡하게 연결되어 있
memodayoungee.tistory.com
DFS와 BFS
그래프의 탐색은 하나의 정점에서 시작하여 모든 정점들을 한 번씩 방문(탐색)하는 것이 목적이다. 그래프의 데이터는 선형구조처럼 정렬되어 있지 않아, 하나씩 모두 방문하여 찾아야 한다. 그래프나 트리를 탐색하기 위해서 DFS와 BFS를 활용할 수 있다.
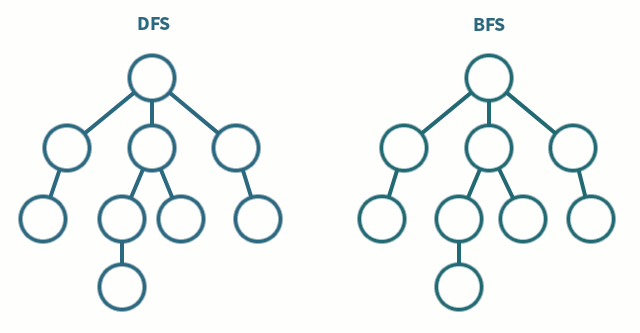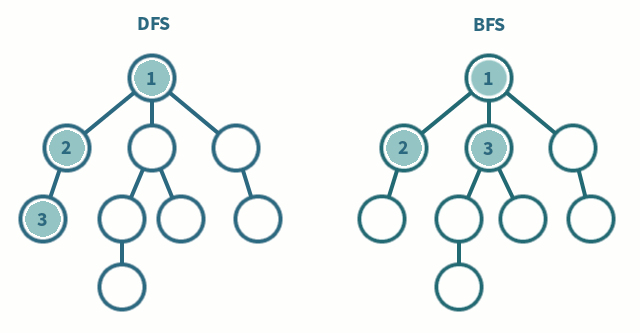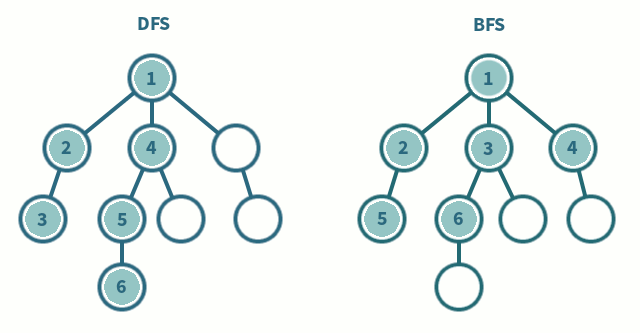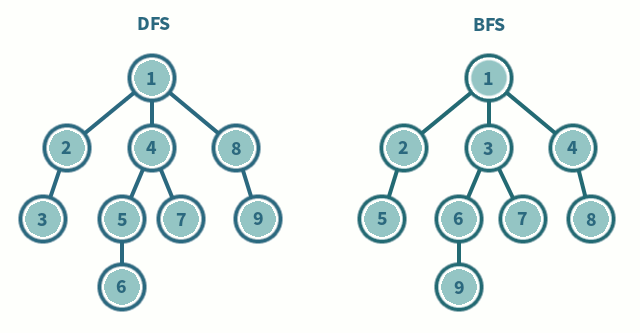
DFS(Depth-First Search: 깊이 우선 탐색)

이름 그대로 DFS는 그래프와 트리의 깊은 부분을 우선적으로 탐색하는 알고리즘 이다. 그림에서와 같이 갈 수 있는 깊이까지 방문하고, 이전 갈림길에서 선택하지 않은 노드들을 방문하여 깊이를 우선으로 탐색하는 알고리즘이다.
DFS는 스택이나 재귀로 구현이 가능하다. 취향 차이겠지만서도 재귀가 스택보다 구현이 더 간단하여 대부분의 사람들은 재귀로 구현하는 듯하다.
BFS(Breadth-First Search: 넓이 우선 탐색)

이름 그대로 BFS는 그래프와 트리의 레벨(넓이) 순으로 탐색하는 알고리즘이다. 인접한 노드들 부터 방문하여 넓게 넓게 뻗아가며 탐색한다고 생각하면 이해가 쉬울 것이다.
BFS는 주로 Queue를 활용해서 구현한다.
DFS vs BFS
그럼 어떨 때 이 두 알고리즘을 활용 할 수 있을까?
- 그래프의 모든 정점을 순회할 때 활용
- DFS와 BFS 중 취향대로 선택하여 문제를 해결할 수 있다.
- 한가지의 경로에 대해서 저장해야 한다.
- BFS는 인접한 노드들 모두를 순회하기 때문에 DFS를 활용해야 한다.
- 경로 이동 시, 가중치가 붙거나 제약이 있을 경우
- DFS를 활용하
- 최단 거리 구하기
- DFS는 처음으로 발견되는 해답이 최단거리가 아닐 수도 있다. 때문에 최악의 경우 마지막으로 순회하는 경로가 최단 거리일 수 있으므로 DFS보다는 BFS를 활용해야 한다. BFS는 너비를 우선으로 탐색하기 때문에 먼저 찾아지는 해답이 곧 최단거리이다.
DFS, BFS 예시
DFS를 구현할 때, 방법이 4가지가 있다.
- 인접 행렬 + stack
- 인접 행렬 + 재귀 구조
- 인접 리스트 + stack
- 인접 리스트 + 재귀 구조
BFS를 구현할 때는, 방법이 2가지이다.
- 인접 행렬 + Queue
- 인접 리스트 + Queue
인접 행렬의 시간 복잡도는 O(n^2), 인접 리스트의 시간 복잡도는 O(n+e) 이다. 고로 밑의 예시는 인접 리스트를 선택했으며 비교적 간단한 재귀를 활용하여 구현되었다.
import java.util.*;
class Graph{
int v;
ArrayList<ArrayList<Integer>> adj;
Graph(int v){
this.v =v;
adj = new ArrayList<ArrayList<Integer>>();
for(int i = 0; i <= v; i++){
adj.add(new ArrayList<Integer>());
}
}
void addEdge(int v, int w){ adj.get(v).add(w); }
// 최솟값부터 들리기 때문에 정렬함
void sortNode(){
for(int i = 1; i <= this.v; i++){
Collections.sort(adj.get(i));
}
}
void DFS(int v){
boolean [] visited = new boolean[this.v + 1];
DFSUtil(v, visited);
}
void DFSUtil(int v, boolean[] visited){
visited[v] = true;
System.out.print(v + " ");
Iterator<Integer> it = adj.get(v).listIterator();
while(it.hasNext()){
int n = it.next();
if(!visited[n]){
DFSUtil(n, visited);
}
}
}
void BFS(int s){
boolean [] visited = new boolean[this.v+1];
Queue<Integer> queue = new LinkedList<>();
visited[s] = true;
queue.offer(s);
while(!queue.isEmpty()){
s = queue.poll();
System.out.print(s + " ");
Iterator<Integer> it = adj.get(s).listIterator();
while(it.hasNext()){
int n = it.next();
if(!visited[n]){
visited[n] = true;
queue.add(n);
}
}
}
}
}
참고
설명이 잘되어 있는 블로그 링크를 따로 달아두고 가겠다.(내가 다시 찾아볼 것 같음)
'Algorithm > 알고리즘 개념' 카테고리의 다른 글
| [알고리즘] 최소 신장 트리 - Prim, Kruskal Algorithm(프림, 크루스칼 알고리즘) (0) | 2023.04.05 |
|---|---|
| [알고리즘] Union-Find Algorithm (유니온 파인드 알고리즘) (0) | 2023.04.04 |
| [알고리즘] Dijkstra Algorithm (다익스트라 알고리즘) (0) | 2023.04.04 |
| [알고리즘] Greedy Algorithm(탐욕 알고리즘) (0) | 2023.04.03 |
| [알고리즘] 01. 비트마스크(Bit mask) (2) | 2023.02.27 |
